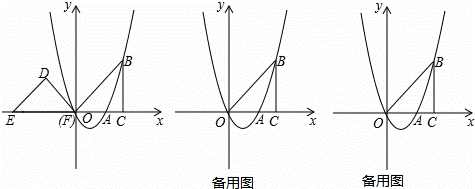
如图,抛物线y=ax2+bx(a≠0)经过点A(2,0),点B(3,3),BC⊥x轴于点C,连接OB,等腰直角三角形DEF的斜边EF在x轴上,点E的坐标为(﹣4,0),点F与原点重合
2024-10-20 05:26:41
如图,抛物线y=ax2+bx(a≠0)经过点A(2,0),点B(3,3),BC⊥x轴于点C,连接OB,等腰直角三角形DEF的斜边EF在x轴上,点E的坐标为(﹣4,0),点F与原点重合
(1)求抛物线的解析式并直接写出它的对称轴;
(2)△DEF以每秒1个单位长度的速度沿x轴正方向移动,运动时间为t秒,当点D落在BC边上时停止运动,设△DEF与△OBC的重叠部分的面积为S,求出S关于t的函数关系式;
(3)点P是抛物线对称轴上一点,当△ABP时直角三角形时,请直接写出所有符合条件的点P坐标.
最佳答案
解:(1)根据题意得,
解得a=1,b=﹣2,
∴抛物线解析式是y=x2﹣2x,
对称轴是直线x=1;
(2)有3中情况:
①当0≤t≤3时,△DEF与△OBC重叠部分为等腰直角三角形,如图1:
S=;
②当3<t≤4时,△DEF与△OBC重叠部分是四边形,如图2:
S=;
③当4<t≤5时,△DEF与△OBC重叠部分是四边形,如图3:
S=;
(3)当△ABP时直角三角形时,可得符合条件的点P坐标为(1,1)或(1,2)或(1,)或(1,).
2024-10-20 05:26:41
赞 709踩 0
