两个三角板ABC，DEF，按如图所示的位置摆放，点B与点D重合，边AB与边DE在同一条直线上（假设图形中所有的点，线都在同一平面内）．其中，∠C=∠DEF=90°，∠ABC=∠F=30°，AC=DE=
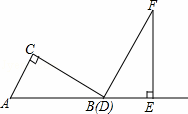
两个三角板ABC
，DEF，按如图所示的位置摆放，点B与点D重合，边AB与边DE在同一条直线上（假设图形中所有的点，线都在同一平面内）．其中，∠C=∠DEF=90°，∠ABC=∠F=30°，AC=DE=6cm．现固定三角板DEF，将三角板ABC沿射线DE方向平移，当点C落在边EF上时停止运动．设三角板平移的距离为x（cm），两个三角板重叠部分的面积为y（cm2）．
（1）当点C落在边EF上时，x= cm；
（2）求y关于x的函数解析式，并写出自变量x的取值范围；
（3）设边BC的中点为点M，边DF的中点为点N．直接写出在三角板平移过程中，点M与点N之间距离的最小值．
最佳答案
解：（1）如图1所示：作CG⊥AB于G点．，
在Rt△ABC中，由AC=6，∠ABC=30，得
BC==6．
在Rt△BCG中，BG=BC•cos30°=9．
四边形CGEH是矩形，
CH=GE=BG+BE=9+6=15cm，
故答案为：15；
（2）①当0≤x＜6时，如图2所示．，
∠GDB=60°，∠GBD=30°，DB=x，得
DG=x，BG=x，重叠部分的面积为y=DG•BG=×x×x=x2
②当6≤x＜12时，如图3所示．，
BD=x，DG=x，BG=x，BE=x﹣6，EH=（x﹣6）．
重叠部分的面积为y=S△BDG﹣S△BEH=DG•BG﹣BE•EH，
即y=×x×x﹣（x﹣6）（x﹣6）
化简，得y=﹣x2+2x﹣6；
③当12＜x≤15时，如图4所示．，
AC=6，BC=6，BD=x，BE=（x﹣6），EG=（x﹣6），
重叠部分的面积为y=S△ABC﹣S△BEG=AC•BC﹣BE•EG，
即y=×6×6﹣（x﹣6）（x﹣6），
化简，得y=18﹣（x2﹣12x+36）=﹣x2+2x+12；
综上所述：y=；
（3）如图5所示作NG⊥DE于G点．，
点M在NG上时MN最短，
NG是△DEF的中位线，
NG=EF=．
MB=CB=3，∠B=30°，
MG=MB=，
MN最小=3﹣=．