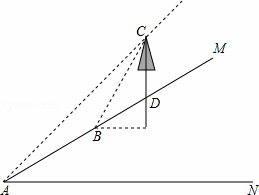
张老师利用休息时间组织学生测量山坡上一棵大树CD的高度，如图，山坡与水平面成30°角（即∠MAN=30°），在山坡底部A处测得大树顶端点C的仰角为45°，沿坡面前进20米，到达B处，又测得树顶端点C的
2024-10-20 05:26:18
张老师利用休息时间组织学生测量山坡上一棵大树CD的高度，如图，山坡与水平面成30°角（即∠MAN=30°），在山坡底部A处测得大树顶端点C的仰角为45°，沿坡面前进20米，到达B处，又测得树顶端点C的仰角为60°（图中各点均在同一平面内），求这棵大树CD的高度（结果精确到0.1米，参考数据：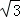
≈1.732）
最佳答案
解：如图，过B作BE⊥CD交CD延长线于E，
∵∠CAN=45°，∠MAN=30°，
∴∠CAB=15°
∵∠CBD=60°，∠DBE=30°，
∴∠CBD=30°，
∵∠CBE=∠CAB+∠ACB，
∴∠CAB=∠ACB=15°，
∴AB=BC=20，
在Rt△BCE中，∠CBE=60°，BC=20，
∴CE=BCsin∠CBE=20×BE=BCcos∠CBE=20×0.5=10，
在Rt△DBE中，∠DBE=30°，BE=10，
∴DE=BEtan∠DBE=10×，
∴CD=CE﹣DE=≈11.5，
答：这棵大树CD的高度大约为11.5米．
2024-10-20 05:26:18
赞 6847踩 0