已知四边形ABCD是正方形，等腰直角△AEF的直角顶点E在直线BC上（不与点B，C重合），FM⊥AD，交射线AD于点M．
已知四边形ABCD是正方形，等腰直角△AEF的直角顶点E在直线BC上（不与点B，C重合），FM⊥AD，交射线AD于点M．
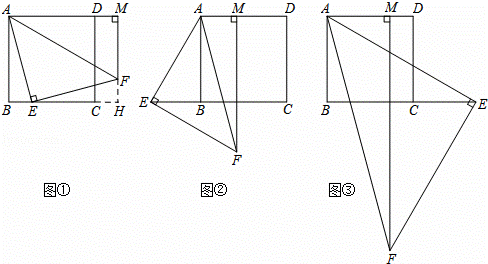
（1）当点E在边BC上，点M在边AD的延长线上时，如图①，求证：AB+BE=AM；
（提示：延长MF，交边BC的延长线于点H．）
（2）当点E在边CB的延长线上，点M在边AD上时，如图②；当点E在边BC的延长线上，点M在边AD上时，如图③．请分别写出线段AB，BE，AM之间的数量关系，不需要证明；
（3）在（1），（2）的条件下，若BE=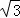
，∠AFM=15°，则AM= 3﹣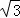或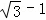
．
最佳答案
（1）证明：如图①，延长MF，交边BC的延长线于点H，
∵四边形ABCD是正方形，FM⊥AD，
∴∠ABE=90°，∠EHF=90°，四边形ABHM为矩形，
∴AM=BH=BE+EH
∵△AEF为等腰直角三角形，
∴AE=AF，∠AEB+∠FEH=90°，
∵∠EFH+∠FEH=90°，
∴∠AEB=∠EFH，
在△ABE与△EHF中，
，
∴△ABE≌△EHF（AAS），
∴AB=EH，
∵AM=BH=BE+EH，
∴AM=BE+AB，即AB+BE=AM；
（2）解：如图②，∵∠AEB+∠FEH=90°，∠AEB+∠EAB=90°，
∴∠FEH=∠EAB，
在△ABE与△EHF中，
，
∴△ABE≌△EHF（AAS），
∴AB=EH=EB+AM；
如图③∠BAE+∠AEB=90°，∠AEB+∠HEF=90°，
∴∠BAE=∠HEF，
在△ABE与△EHF中，
，
∴△ABE≌△EHF（AAS），
∴AB=EH，
∴BE=BH+EH=AM+AB；
（3）解：如图①，∵∠AFM=15°，∠AFE=45°，
∴∠EFM=60°，
∴∠EFH=120°，
在△EFH中，
∵∠FHE=90°，∠EFH=120°，
∴此情况不存在；
如图②，∵∠AFM=15°，∠AFE=45°，
∴∠EFH=60°，
∵△ABE≌△EHF，
∴∠EAB=∠EFH=60°，
∵BE=，
∴AB=BE•tan60°=×=3，
∵AB=EB+AM，
∴AM=AB﹣EB=3﹣；
如图③，∵∠AFM=15°，∠AFE=45°，
∴∠EFH=45°﹣15°=30°，
∴∠AEB=30°，
∵BE=，
∴AB=BE•tan30°==1，
∵BE=AM+AB，
AM=BE﹣AB=，
故答案为：3﹣或．