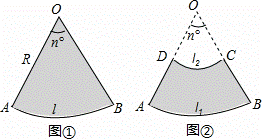
如图①，半径为R，圆心角为n°的扇形面积是S扇形=，由弧长l=，得S扇形==••R=lR．通过观察，我们发现S扇形=lR类似于S三角形=×底×高．
2024-10-20 05:25:06
如图①，半径为R，圆心角为n°的扇形面积是S扇形=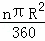
，由弧长l=
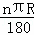，得S扇形==
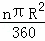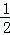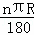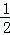••R=lR．通过观察，我们发现S扇形=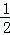lR类似于S三角形=
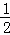×底×高．
类比扇形，我们探索扇环（如图②，两个同心圆围成的圆环被扇形截得的一部分交作扇环）的面积公式及其应用．
（1）设扇环的面积为S扇环，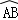
的长为l1，
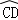的长为l2，线段AD的长为h（即两个同心圆半径R与r的差）．类比S梯形=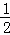×（上底+下底）×高，用含l1，l2，h的代数式表示S扇环，并证明；
（2）用一段长为40m的篱笆围成一个如图②所示的扇环形花园，线段AD的长h为多少时，花园的面积最大，最大面积是多少？
最佳答案
（1）S扇环=（l1﹣l2）h，
证明：设大扇形半径为R，小扇形半径为r，圆心角度数为n，则由l=，得R=，r=
所以图中扇环的面积S=×l1×R﹣×l2×r
=l1•﹣l2•
=（l12﹣l22）
=（l1+l2）（l1﹣l2）
=••（R﹣r）（l1﹣l2）
=（l1﹣l2）（R﹣r）
=（l1+l2）h，
故猜想正确．
（2）解：根据题意得：l1+l2=40﹣2h，
则S扇环=（l1+l2）h
=（40﹣2h）h
=﹣h2+20h
=﹣（h﹣10）2+100
∵﹣1＜0，
∴开口向下，有最大值，
当h=10时，最大值是100，
即线段AD的长h为10m时，花园的面积最大，最大面积是100m2．
2024-10-20 05:25:06
赞 9101踩 0