如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm
2024-10-20 05:24:16
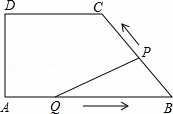
如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t s,解答下列问题:
(1)当t为何值时,P,Q两点同时停止运动?
(2)设△PQB的面积为S,当t为何值时,S取得最大值,并求出最大值;
(3)当△PQB为等腰三角形时,求t的值.
最佳答案
解:(1)作CE⊥AB于E,
∵DC∥AB,DA⊥AB,
∴四边形AFVE是矩形,
∴AE=DE=5,CE=AD=4,
∴BE=3,
∴BC=,
∴BC<AB,
∴P到C时,P、Q同时停止运动,
∴t=(秒),
即t=5秒时,P,Q两点同时停止运动.
(2)由题意知,AQ=BP=t,
∴QB=8﹣t,
作PF⊥QB于F,则△BPF~△BCE,
∴,即,
∴BF=,
∴S=QB•PF=×(8﹣t)==﹣(t﹣4)2+(0<t≤5),
∵﹣<0,
∴S有最大值,当t=4时,S的最大值是;
(3)∵cos∠B=,
∴BF=t•cos∠B=,
∴QF=AB﹣AQ﹣BF=8﹣,
∴QP===4
①当PQ=PB时,即QP═4,解得t=(舍去负值)
∵t=>5,不合题意,
②当PQ=BQ时,即4=8﹣t,
解得:t1=0(舍去),t2=,
③当QB=BP,即8﹣t=t,
解得:t=4.
综上所述:当t=秒或t=4秒时,△PQB为等腰三角形.
2024-10-20 05:24:16
赞 204踩 0
