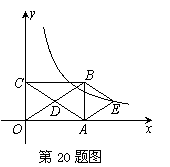
如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,BE∥AC,AE∥OB.
2024-10-20 05:24:13
如图,在平面直角坐标系中,矩形OA BC的对角线OB,AC相交于点D,BE∥AC,AE∥OB.
BC的对角线OB,AC相交于点D,BE∥AC,AE∥OB.
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式.
 |
最佳答案
(1) 证明:∵ BE∥AC,AE∥OB,
∴四边形AEBD是平行四边形.
又∵四边形OABC是矩形,
∴OB=AC,且互相平分,
∴DA=DB.
∴四边形AEBD是菱形.
(2)连接DE,交AB于点F.
由(1)四边形AEBD是菱形,
∴AB与DE互相垂直平分.
又∵OA=3,OC=2,
∴EF=DF=OA= ,AF=AB=1 .
∴E点坐标为( ,1).
设反比例函数解析式为 ,
把点E( ,1)代入得.
∴所求的反比例函数解析式为.
2024-10-20 05:24:13
赞 1765踩 0
