如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边中线,点D,E分别在边AC和BC上,DB=DE,EF⊥AC于点F,以下结论:
2024-10-20 05:23:59
如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边中线,点D,E分别在边AC和BC上,DB=DE,EF⊥AC于点F,以下结论:
(1)∠DBM=∠CDE; (2)S△BDE<S四边形BMFE;
(3)CD•EN=BN•BD; (4)AC=2DF.
其中正确结论的个数是( )
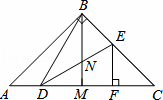
A. 1 B. 2 C. 3 D. 4
最佳答案
C. 解:(1)设∠EDC=x,则∠DEF=90°﹣x
∴∠DBE=∠DEB=∠EDC+∠C=x+45°,
∵BD=DE,
∴∠DBM=∠DBE﹣∠MBE=45°+x﹣45°=x.
∴∠DBM=∠CDE,故(1)正确;
(2)在Rt△BDM和Rt△DEF中,
,
∴Rt△BDM≌Rt△DEF.
∴S△BDM=S△DEF.
∴S△BDM﹣S△DMN=S△DEF﹣S△DMN,即S△DBN=S四边形MNEF.
∴S△DBN+S△BNE=S四边形MNEF+S△BNE,
∴S△BDE=S四边形BMFE,故(2)错误;
(3)∵∠BNE=∠DBM+∠BDN,∠BDM=∠BDE+∠EDF,∠EDF=∠DBM,
∴∠BNE=∠BDM.
又∵∠C=∠NBE=45°
∴△DBC∽△NEB.
∴,
∴CD•EN=BN•BD;故(3)正确;
(4)∵Rt△BDM≌Rt△DEF,
∴BM=DF,
∵∠B=90°,M是AC的中点,
∴BM=.
∴DF=,故(4)正确.
2024-10-20 05:23:59
赞 7462踩 0
