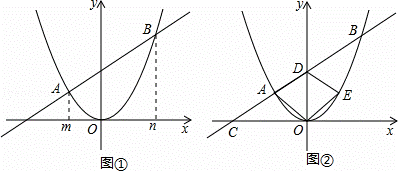
如图①,一次函数y=kx+b的图象与二次函数y=x2的图象相交于A,B两点,点A,B的横坐标分别为m,n(m<0,n>0).
如图①,一次函数y=kx+b的图象与二次函数y=x2的图象相交于A,B两点,点A,B的横坐标分别为m,n(m<0,n>0).
(1)当m=﹣1,n=4时,k= ,b= ;
当m=﹣2,n=3时,k= ,b= ;
(2)根据(1)中的结果,用含m,n的代数式分别表示k与b,并证明你的结论;
(3)利用(2)中的结论,解答下列问题:
如图②,直线AB与x轴,y轴分别交于点C,D,点A关于y轴的对称点为点E,连接AO,OE,ED.
①当m=﹣3,n>3时,求 的值(用含n的代数式表示);
的值(用含n的代数式表示);
②当四边形AOED为菱形时,m与n满足的关系式为 n=﹣2m ;
当四边形AOED为正方形时,m= ﹣1 ,n= 2 .
最佳答案
解:(1)当x=﹣1时,y=x2=1,则A(﹣1,1);当x=4时,y=x2=16,则B(4,16),
把A(﹣1,1)、B(4,16)分别代入y=kx+b得,解得;
当x=﹣2时,y=x2=4,则A(﹣2,4);当x=3时,y=x2=9,则B(3,9),
把A(﹣2,4)、B(3,9)分别代入y=kx+b得,解得;
故答案为:3,4;1,6;
(2)k=m+n,b=﹣mn.理由如下:
把A(m,m2),B(n,n2)代入y=kx+b得,解得;
(3)①当m=﹣3时,A(﹣3,9),
∵点A关于y轴的对称点为点E,
∴E(3,9),
∵k=m+n,b=﹣mn,
∴k=﹣3+n,b=3n,
∴直线AB的解析式为y=(﹣3+n)x+3n,则D(0,3n),
当y=0时,(﹣3+n)x+3n=0,解得x=,则C(,0),
∴==(n>3);
②连结AE交OD于P,如图②,
∵点A(m,m2)关于y轴的对称点为点E,
∴E(﹣m,m2),
∴OP=m2,
∵k=m+n,b=﹣mn,
∴D(0,﹣mn),
若四边形AOED为菱形,则OP=DP,即﹣mn=2m2,所以n=﹣2m;
若四边形AOED为正方形,则OP=AP,即﹣m=m2,解得m=﹣1,所以n=﹣2m=2.
