已知抛物线 y=mx2+4x+2m与x轴交于点A(,0)、B(,0),且.
已知抛物线 y= mx2+4x+2m与x轴交于点A(
mx2+4x+2m与x轴交于点A( ,0)、B(
,0)、B( ,0),且
,0),且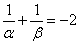 .
.
(1)求抛物线的解析式.
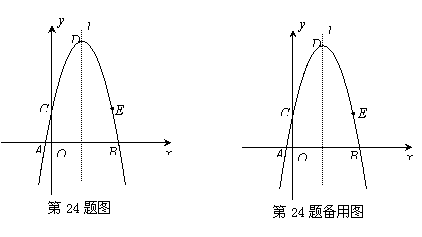
(2)抛物线的对称轴为l,与y轴的交点为C,顶点为D,点C关于l对称点为E.是否存在 x轴上的点M、y轴上的点N,使四边形DNME的周长最小?若存在,请画出图形(保留作图痕迹),并求出周长的最小值;若不存在,请说明理由.
(3)若点P在抛物线上,点Q在x轴上,当以点D、E、P、Q为顶点的四边形为平行四边形时,求点P的坐标.
 |
最佳答案
(1)由题意可知,, 是方程 的两根,由根与系数的关系可得,+= ,=-2.
∵ ,
∴ .即:.
∴m=1.
∴抛物线解析式为.
(2) 存在x轴,y轴上的点M,N,使得四边形DNME的周长最小.
∵,
∴抛物线的对称轴为 ,顶点D的坐标为(2,6).
又抛物线与y轴交点C的坐标为(0,2),点E与点C关于对称,
∴E点坐标为(4,2).
作点D关于y轴的对称点D′,作点E关于x轴的对称点E′,
则D′坐标为(-2,6),E′坐标为(4,-2).连接D′E′,交x轴于M,交y轴与N.
此时,四边形DNME的周长最小为D′E′+DE.(如图1所示)
延长E′E, D′D交于一点F,在Rt△D′E′F中,D′F=6,E′F=8.
∴D′E′= = .
设对称轴与CE交于点G,在Rt△DG E中,DG=4,EG=2.
∴DE= =.
∴四边形DNME的周长的最小值为
10+ .
(3)如图2, P为抛物线上的点,过P作PH⊥x轴,垂足为H.若以点D、E、P、Q为顶点的四边形为平行四边形,则△PHQ≌△DGE.
∴PH=DG=4.
即 =4.
∴当y=4时, =4,解得
当y=-4时, =-4,解得.
∴点P的坐标为( ,4),(,4),(,-4),(,-4).
