已知四边形ABCD内接于⊙O,∠ADC=90°,∠DCB<90°,对角线AC平分∠DCB ,
已知四边形ABCD内接于⊙O,∠ADC=90°,∠DCB<90°,对角线AC平分∠DCB ,
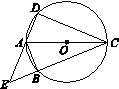
延长DA,CB相交于点E.
(1)如图11,EB=AD,求证:△ABE是等腰直角三角形;
(2)如图12,连接OE,过点E作直线EF,使得∠OEF=30°.
当∠ACE≥30°时,判断直线EF与⊙O的位置关系,并说明理由.
 | |||
 | |||
最佳答案
(1)证明:∵四边形ABCD内接于⊙O,∠ADC=90°,
∴∠ABC=90°.
∴∠ABE=90°.
∵AC平分∠DCB,
∴∠ACB=∠ACD.
∴AB=AD.
∵EB=AD,
∴EB=AB.
∴△ABE是等腰直角三角形.
(2)直线EF与⊙O相离.
证明:过O作OG⊥EF,垂足为G.
在Rt△OEG中,
∵∠OEG=30°,
∴OE=2OG.
∵∠ADC=90°,
∴AC是直径.
设∠ACE=,AC=2r.
由(1)得∠DCE=2,
又∠ADC=90°,
∴∠AEC=90°-2.
∵≥30°,
∴(90°-2)-≤0.
∴∠AEC≤∠ACE.
∴AC≤AE.
在△AEO中,∠EAO=90°+,
∴∠EAO>∠AOE.
∴EO>AE.
∴EO-AE>0.
由AC≤AE得AE-AC≥0.
∴EO-AC=EO+AE-AE-AC
=(EO-AE)+(AE-AC)>0.
∴EO>AC.
即2OG≥2r.
∴OG>r.
∴直线EF与⊙O相离.
