如图所示:三角形ABC的面积为10平方厘米,AE=DE,BD=3CD.那么阴影部分的面积是3.753.75平方厘米.
2024-10-20 05:20:39
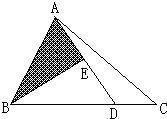 如图所示:三角形ABC的面积为10平方厘米,AE=DE,BD=3CD.那么阴影部分的面积是
如图所示:三角形ABC的面积为10平方厘米,AE=DE,BD=3CD.那么阴影部分的面积是3.75
3.75
平方厘米.最佳答案
分析:观察图形:AE=DE,BD=3CD,根据高一定时,三角形的面积与底成正比例的性质,可得:阴影部分的面积=
1
2
×三角形ABD的面积;三角形ABD的面积=
3
4
×三角形ABC的面积;由此可得阴影部分的面积=
3
8
×三角形ABC的面积,代入三角形ABC的面积即可解答问题.解答:解:根据题干分析可得:阴影部分的面积=
1
2
×三角形ABD的面积;三角形ABD的面积=
3
4
×三角形ABC的面积;所以阴影部分的面积=
3
8
×三角形ABC的面积,因为三角形ABC的面积是10平方厘米,所以阴影部分的面积是:10×
3
8
=3.75(平方厘米),答:阴影部分的面积是3.75平方厘米.故答案为:3.75.点评:此题考查了高一定时,三角形的面积与底成正比例的性质的灵活应用.
2024-10-20 05:20:39
赞 3055踩 0
