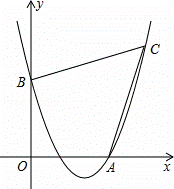
)如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).
2024-10-20 05:17:54
)如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).
(1)求抛物线的表达式;
(2)证明:四边形AOBC的两条对角线互相垂直;
(3)在四边形AOBC的内部能否截出面积最大的▱DEFG?(顶点D,E,F,G分别在线段AO,OB,BC,CA上,且不与四边 形AOBC的顶点重合)若能,求出▱DEFG的最大面积,并求出此时点D的坐标;若不能,请说明理由.
形AOBC的顶点重合)若能,求出▱DEFG的最大面积,并求出此时点D的坐标;若不能,请说明理由.
最佳答案
解:(1)设该抛物线的解析式为y=ax2+bx+c,
根据题意得,解得,
∴抛物线的表达式为y=x2﹣x+4;
(2)如图1,连结AB、OC,
∵A(4,0),B(0,4),C(6,6),
∴OA=4,OB=4,CB==2,CA==2,
∴OA=OB,CA=CB,
∴OC垂直平分AB,
即四边形AOBC的两条对角线互相垂直;
(3)能.
如图2,AB==4,OC==6,设D(t,0),
∵四边形DEFG为平行四边形,
∴EF∥DG,EF=DG,
∵OC垂直平分AB,
∴△OBC与△OAC关于OC对称,
∴EF和DG为对应线段,
∴四边形DEFG为矩形,DG∥OC,
∴DE∥AB,
∴△ODE∽△OAB,
∴=,即=,解得DE=t,
∵DG∥OC,
∴△ADG∽△AOC,
∴=,即=,解得DG=(4﹣t),
∴矩形DEFG的面积=DE•DG=t•(4﹣t)=﹣3t2+12t=﹣3(t﹣2)2+12,
当t=2时,平行四边形DEFG的面积最大,最大值为12,此时D点坐标为(2,0).
2024-10-20 05:17:54
赞 1156踩 0
